Document details

Abstract
In satellite maneuver detection, achieving accurate and reliable uncertainty propagation is essential. The accuracy of these predictions relies significantly on the choice of state representation and propagation methodology, particularly for computing the single Gaussian-based k2 anomaly detection metric. However, traditional Cartesian representations face significant limitations in maintaining Gaussianity within the propagated probability density functions (PDFs) over extended intervals. This study addresses these limitations by examining the potential of alternative curvilinear state representations to improve uncertainty realism for long-term propagation.
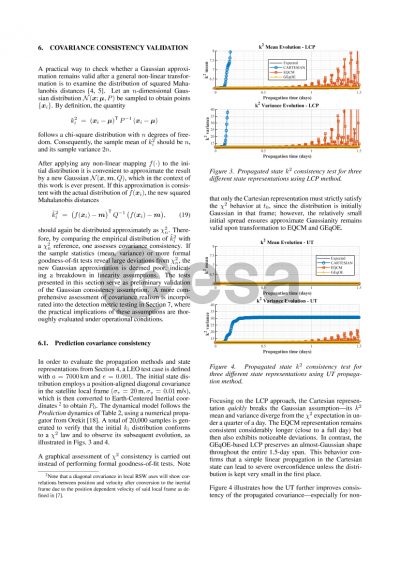
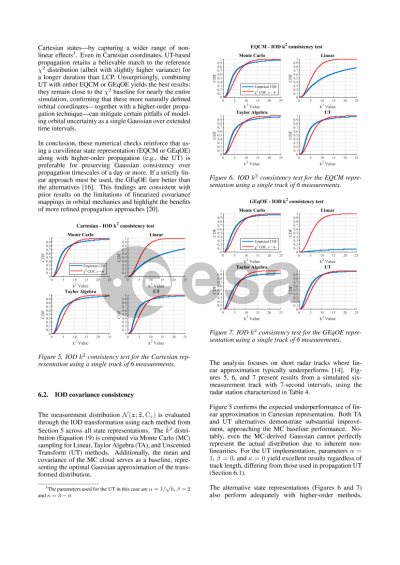
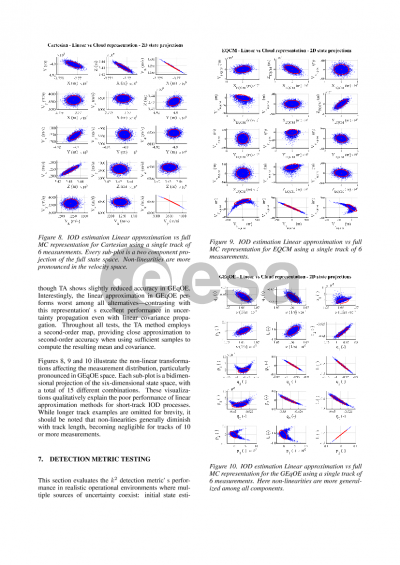
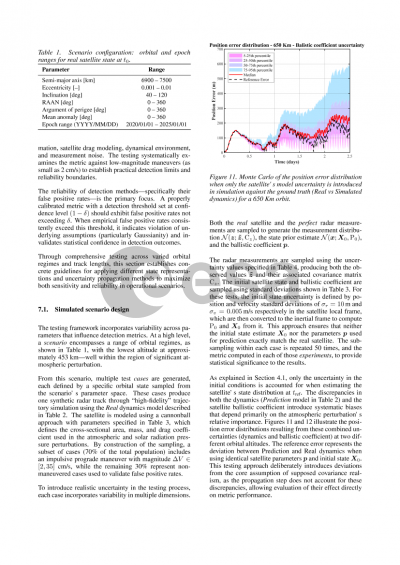
The research begins with a focused evaluation of two propagation techniques: linear propagation and the Unscented Transform (UT). These techniques are initially tested with both Cartesian and Modified Equidistant Cylindrical (EQCM) representations to assess their fidelity in approximating the true PDF, represented by Monte Carlo samples. Given an initial Gaussian uncertainty, we examine the propagated samples through the squared Mahalanobis distance (k2) from the central state. Ideally, the distribution of the k2 samples should conform to a chi-squared distribution, with known mean and variance, over time. Among the methods tested, EQCM, particularly when paired with UT propagation, maintained this theoretical consistency more effectively than Cartesian coordinates, with only slight deviations from the ideal k2 values. The findings indicate that the EQCM representation, as outlined by Vallado (Curvilinear coordinate transformations for relative motion), can sustain Gaussianity over longer periods when compared to Cartesian representations, especially when relying on linear propagation of the covariance matrix. Specifically, results from our analysis show that EQCM’s design is more appropriate for the non-linear transformations of orbital mechanics, as it explicitly sets its axis to conform with the Keplerian orbit. Although Cartesian representations can capture the initial uncertainty, they quickly deviate from Gaussianity in both position and velocity as time elapses. EQCM's structure reduces this deviation, allowing for a more robust and extended interval of valid Gaussian approximation, a feature that is critical in maintaining accuracy and reliability in anomaly detection for maneuver tracking.
To broaden this analysis, the presented work will incorporate additional curvilinear state representations, including the Gauss von Mises (GVM) and Generalized Equinoctial Orbital Elements (GEqOEs). Each of these representations offers distinct advantages for uncertainty propagation, potentially extending Gaussianity retention even further than EQCM. Additionally, the analytical Jacobians available for these representations enable efficient linear propagation, offering a computationally feasible alternative to the UT, with comparable levels of accuracy in certain scenarios. By comparing EQCM, GVM, and GEOEs, this study aims to provide a comprehensive view of the trade-offs among these state representations for uncertainty propagation, highlighting the strengths and limitations of each approach. The different methods are then tested for anomaly detection using estimated states from simulated radar tracks with a novel IOD technique. The results will offer practical recommendations for selecting appropriate state representations based on accuracy, computational efficiency, and uncertainty propagation robustness.
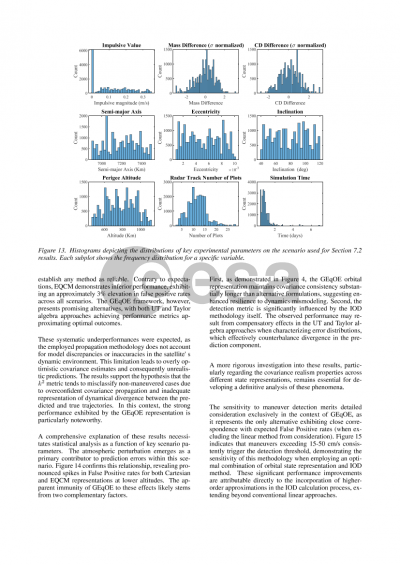
Preview