Gaussian Mixture-Unscented Transform propagation during re-entry fragmentation for impact uncertainty quantification

Motivated by the ever-increasing space debris population in LEO and subsequent re-entry events, risk analysis of the effects of uncontrolled re-entry on-ground is considered a key component of modern space debris mitigation strategies.

A standard approach of quantifying the uncertainty associated with re-entry makes significant use of Monte Carlo (MC) campaigns but the heavy computation burden of invoking MC means that physical models applied to re-entry modelling in terms of aerothermodynamics, structures and flight dynamics must often be necessarily limited. This work proposes the use of nonlinear propagation techniques commonly applied in on-orbit uncertainty quantification as a means to acquire results without needing to expend significant resources on an MC campaign.

The Unscented Transform (UT) significantly reduces the requisite function evaluations necessary to propagate a probability distribution through a nonlinear function. This is achieved by sacrificing information on the distribution beyond the first two statistical moments. If a distribution can be safely assumed (almost always as a normal distribution), the UT presents significant computational savings over MC. Unfortunately, re-entry processes can cause positional uncertainty to deviate significantly from Gaussian descriptions, thus the motivation for applying a Gaussian Mixture Model (GMM) to approximate a non-Gaussian distribution as a weighted sum of a “library” of Gaussians. These two propagation techniques together comprise the hybrid model known as GMM-UT.

The common use of covariance matrices in orbital uncertainty propagation enables interoperability between standard orbital methods and the proposed re-entry uncertainty propagation. Additionally, the lower computational expense provides the opportunity to utilise more sophisticated physical models for re-entry, be that in terms of higher fidelity aerothermodynamical computation, advanced structural models or in this case where a larger quantity of fragments and fragmentation events than would usually be feasible for MC propagation can be analysed.

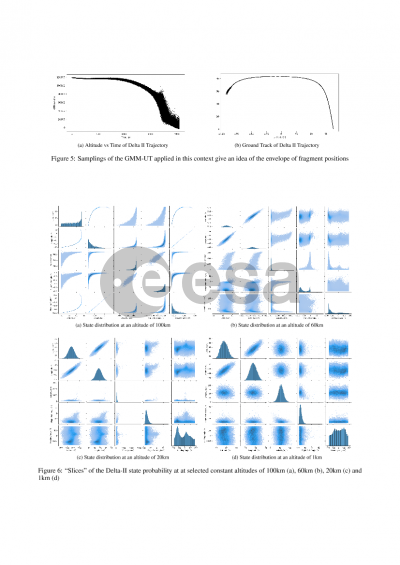
In this work, the comparative cheapness of GMM-UT is leveraged to propagate a cluster of spacecraft fragments simultaneously whilst still computing the aerodynamics and aero-induced heating on these bodies. This is performed using the TransatmospherIc flighT simulAtioN tool (TITAN), a code developed by the University of Strathclyde for the purpose of simulating hypersonic re-entries utilising models of multiple fidelities.

TITAN’s panel-code models approximate aerodynamic effects enabling efficient propagation of multivariate uncertain initial conditions in position and velocity. This is done whilst accounting for both purely translational (6 dimensional) and combined translational and rotational uncertainty (12 dimensional).

Results obtained for a more trivial fragmentation case are compared, utilising statistical similarity measures, against conventional Monte Carlo campaigns and single-distribution Unscented Transform propagation. They are used alongside the results obtained for a more complex case to advocate for further exploration of nonlinear propagation as a method for efficient uncertainty quantification during re-entry.