Next-Generation Re-entry Aerothermodynamic Modeling for Space Debris using Deep Learning

Atmospheric re-entry analysis is a critical component to mission planning in order to ensure that the end of a spacecraft’s mission is properly planned. Specifically, it is of upmost importance to ensure that any re-entering spacecraft or debris do not pose any threat to civilians, buildings, or populated areas on the ground. As the volume of spacecraft and other space assets in the Low-Earth Orbit (LEO) environment increases, it is expected that space will be considerably more crowded in the next decade and beyond. Per requirements and recommendations outlined by NASA’s Orbital Debris Program Office (ODPO) to mitigate further pollution of the space environment, satellites are recommended to re-enter Earth’s atmosphere within 25 years of the end of its life. Upon re-entry, spacecraft must not pose a greater than 1:10,000 risk of striking any significant objects or causing any civilian casualties on the ground.

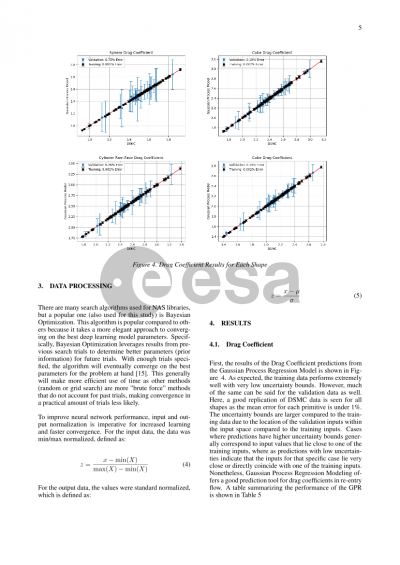
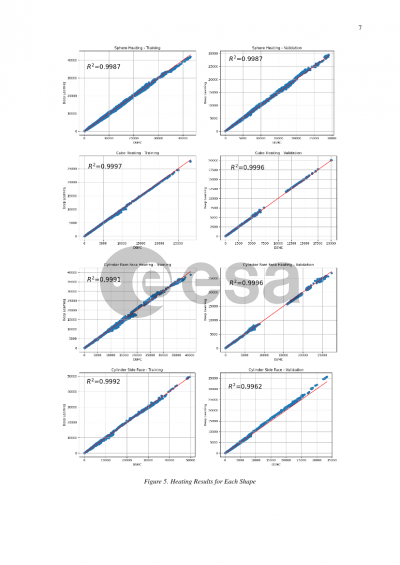
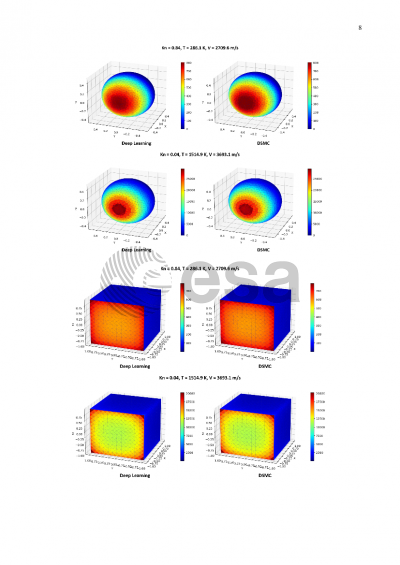
To date, the predominant analysis tools for re-entry assessment are object-oriented codes such as NASA’s ORSAT, CNES’ DEBRISK, and ESA’s SARA. These tools assume a trajectory in which a spacecraft will fragment into multiple shape primitives at a certain altitude, and the following risk analysis is performed on these simple objects. Conversely, spacecraft-oriented tools such as ESA’s SCARAB, simulate the entire spacecraft until demise to determine its risk. Both types of tools determine drag and heating coefficients for risk assessment through the use of semi-empirical and analytical formulations. For finite nose radius objects such as a sphere, closed-form solutions exist for stagnation point heating. For other convex shapes such as cubes, cylinders, and other sharp-edged objects, no closed-form solutions exist, and estimation is achieved with the use of shape factors or bridging functions. These models are quickly evaluated, but the analytical and bridging functions do not have well defined accuracy or uncertainty. High-fidelity modeling tools such as Direct Simulation Monte-Carlo (DSMC) codes can provide numerical estimates for heating and drag distributions over shape primitives given certain flow conditions. However, the main drawback to these tools is computational expense (where analytical formulations excel): The computational resources needed to numerically solve particle motion and surface interactions scales exponentially with increasing atmospheric density.

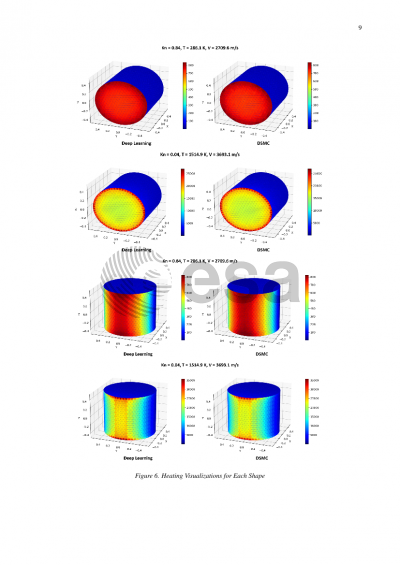
A challenge arises where there is a need to strike a balance between computational cost and accuracy. A tradeoff can be reached through machine (deep) learning techniques by enabling accurate emulation of the numerical solutions for given a set of flow conditions. With a robust framework, re-entry computations can be completed quickly while maintaining the similar accuracy as numerical methods and providing uncertainty estimates, thereby making possible probabilistic analyses through large number of ensemble runs. We present results with models that are able to predict drag and heating coefficients and distributions for a sphere and cube within 5% error and minimal computational cost while only requiring a fraction of a second per flow case.