Document details

Abstract
The ever-increasing amount of uncontrolled space objects, known as space debris, poses a risk to space activities due to possible collisions with operational spacecraft. An accurate prediction of their orbit is needed to prevent damages to infrastructure in orbit and on the ground. In the frame of Spanish SST activities, the S3TOC (Spanish operational centre for SST) is investigating new techniques and methods that are expected to improve current procedures to determine and predict the orbit.
Several estimation techniques have been developed over the years, aiming to accurately determine the orbit of space objects from observations. One can distinguish between batch and sequential estimators, which address two different problems. While the former obtains or improves an epoch state estimate by processing a whole set of observations in each run, sequential estimators process one measurement at a time and yield subsequent estimates of the state vector at the time of each measurement.
In addition, such techniques can be also classified depending on the propagation method they implement. In a numerical propagation, the equations of motion are numerically integrated, leading to accurate results but long computational time. In contrast, analytical methods integrate the equations of motion analytically using approximated closed-form solutions for the orbital motion to speed up the process. This is, however, not always possible and limits the accuracy. Finally, semi-analytical methods (SA) aim to merge advantages of both. All above-mentioned propagation methods can be implemented in the framework of Differential Algebra (DA). DA is a computing technique that uses truncated power series instead of numbers to represent variables.
We present a first operative tool for the orbital determination (OD) of space objects that exploits DA techniques to implement a least squares (LS) method compatible with numerical and semi-analytical propagators. In the above-mentioned context, DA allows us to obtain a polynomial representation of the residuals function on which efficient optimization techniques can be run to determine the optimum. Additionally, DA removes the need to both integrate the variational equations for the state transition matrix and to linearize the measurement functions thus enabling the use of arbitrary dynamics and observation types.
Our effort is mainly focused on the coupling of the resulting DALS solver with the semi-analytical propagator SADA. Semi-analytical propagation methods combine analytical methods and numerical integration techniques, trying to get the best mix of accuracy and efficiency. To this aim, short-periodic motion is filtered out and larger time steps can therefore be used for the integration of the equations of motion. The resulting algorithm (sDALS) benefits from the high efficiency of both the DALS solver and the SADA propagator, while partially sacrificing orbit accuracy. The accuracy and efficiency of sDALS are assessed against a high-fidelity version of the same tool, aDALS, that exploits the numerical AIDA (Accurate Integrator for Debris Analysis) propagator. Both versions are compared against conventional OD techniques. This comparison is done in terms of OD result accuracy and computational cost, and a detailed analysis on the sensitivity of the tool under operative conditions (object parameters availability and OD first guess accuracy) is offered. The whole analysis is performed with real observations, from both telescopes and radars, for objects in LEO, HEO and GEO.
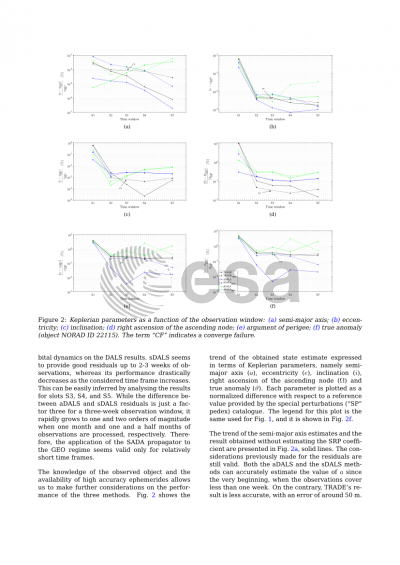
Preview