Initial orbits of LEO objects using radar observations

The space environment is being continuously exposed to risks of on-orbit break-up events and to the growing number of smaller satellites and large constellations, leading to the unavoidable growth of space debris population. Surveillance and tracking of this population remain essential to monitor its evolution and to protect the operational satellites, population and infrastructure on the ground. That drives the need to develop and improve the algorithms in orbit computation.
The “Infinitesimal Angles Method” introduced in (Gronchi et al. 2015)(1) is conceived to compute initial orbits of Low Earth satellites from radar data by applying a correction to the line of sight. We present an extension of this algorithm that includes the Earth oblateness effect in the dynamical model (Ma et al. 2018)(2).
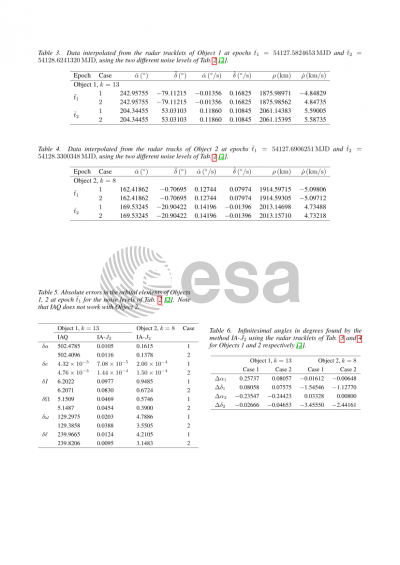
A single observation gives the topocentric position of the satellite at epoch t defined by (t, ρ, α, δ) where ρ is the range, α the right ascension and δ the declination. A set of at least four observations constitutes a tracklet. We assume that the radar observations are collected at short time intervals, the range is accurate and the line-of-sight direction given by α, δ is poorly determined. Considering a pair of radar tracklets, the values of the range (ρ) and the range rate (ρ’) at the mean epochs of these tracklets can be obtained by a polynomial fitting.
To compute an orbit from radar data, one has to determine the values of the angular velocities (α’, δ’) and provide corrections to the angles (denoted by ∆α, ∆δ). The proposed method tries to link two tracklets by solving a system of eight equations in the eight unknowns (∆α_i, ∆δ_i, α’_i, δ’_i), i=1,2, where the subscripts refer to the mean epoch of the tracklets.
The system is composed by the equation of motion projected onto the line of sight at the two mean epochs, a suitable version of Lambert’s equation and an evolution of the Keplerian integrals. The assumed dynamical model is a perturbed Keplerian dynamics where the only perturbation included is the secular effect of the J2 term of the geopotential.
The numerical tests in (Gronchi et al. 2015)(1) showed that the “Infinitesimal Angles Method” is able to correct the errors in the angular measurements supposing the orbital motion is purely Keplerian. The extended method (Ma et al. 2018)(2) is tested for some simulated objects, and compared with the initial algorithm and another method that includes the Earth oblateness (Farnocchia et al. 2010)(3).
(1) G. F. Gronchi, L. Dimare, D. Bracali Cioci, H. Ma, On the computation of preliminary orbits for Earth satellites with radar observations, Monthly Notices of the Royal Astronomical Society, Volume 451, Issue 2, Pages 1883–1891, August 2015.
(2) H. Ma., G. Baù, D. Bracali Cioci, G. F. Gronchi, Preliminary orbits with line-of-sight correction for LEO satellites observed with radar, Celestial Mechanics and Dynamical Astronomy, Volume 130, October 2018.
(3) D. Farnocchia, G. Tommei, A. Milani, A. Rossi, Innovative methods of correlation and orbit determination for space debris. Celestial Mechanics and Dynamical Astronomy, Volume 107, Pages 169–185, April 2010.