Analysis of maneuver errors during the early orbit and station-keeping phases of an electrical satellite

Maneuver uncertainties have a significant impact on an object state vector uncertainty, especially when multiple maneuvers are performed over a short timespan (for example, during post-launch, station-keeping or deorbitation phases using electrical, low-trust maneuvers). They are usually due to nozzle imperfections or faulty propellant reaction, leading to small errors on the magnitude and direction of the thrust. Downstream Space Situational Awareness (SSA) functions --- such as cataloging or collision risk assessment --- usually require propagating state vector uncertainties over long periods of time, and often assume the uncertainty follows a Gaussian distribution in Cartesian space through the entire propagation.

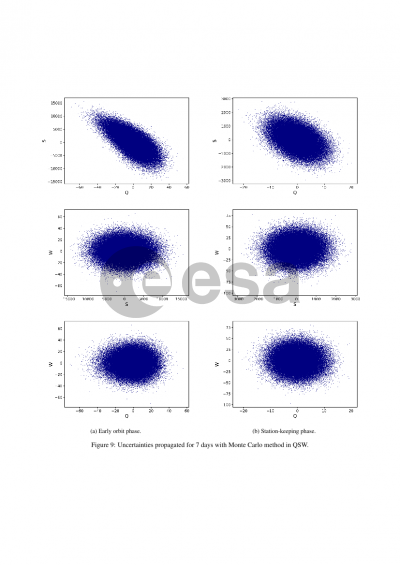
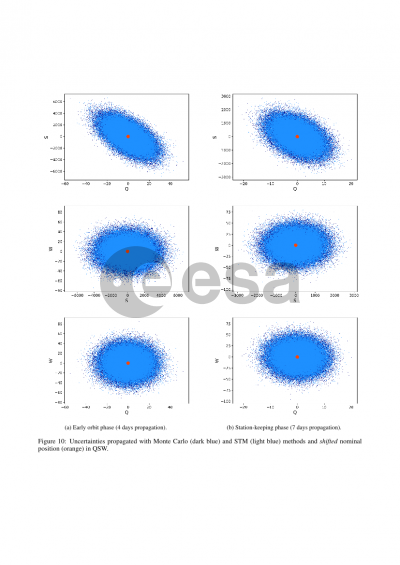
This paper presents the results of a pre-launch study aiming to assess how long such an hypothesis holds during the early orbit and station-keeping phases of a satellite planning to perform respectively 58 and 29 electrical maneuvers with different durations, each phase spread over two days. To that end, the state vector uncertainty computed through a state transition matrix (STM) is compared at different times to the one computed using a Monte Carlo method.

Initial results show the state vector uncertainty remains Gaussian only for a limited period of time. Although the state transition matrix can be used for covariance propagation on this time interval, particular attention should be payed to the representation of maneuvers uncertainties as a matrix, which can be complex since magnitude and direction errors cannot be modeled independently. Moreover, Monte Carlo results reveal the maneuver direction error can have a significant impact on the total uncertainty, depending on its value. The greater the direction error, the more the nominal state vector departs from the perturbed samples, causing the uncertainty to lose its Gaussianity and making state transition matrix propagation unsuitable.