Document details

Abstract
The accurate prediction of the impact region of a reentering space object is a very complex problem. A typical reentry scenario involves three major steps. First, the object leaves its original orbit and starts falling back on Earth. This deorbitation step can take years in the case of a natural reentry or minutes in the case of a controlled deorbitation. The fragmentation step is likely to occur as the object enters more dense layers of the atmosphere, typically at an altitude of 100 kilometers. After fragmentation, parts of the object keep falling while being ablated by the atmosphere before hitting the ground or being entirely burnt by the atmosphere.
The objective of this work is to accurately predict the impact region of the surviving fragments of an object. Due to the complexity of the physics involved during reentry, the scarcity of experiments and the unpredictability of events such as fragmentation, any model trying to predict a reentry features a limited reliability due to simplified assumptions and scarcity of data. In this work, we aim to alleviate this issue by coupling an original uncertainty quantification method with a space object reentry software developed by Airbus Safran Launchers in order to estimate the reliability of the numerical predictions. Although Uncertainty Quantification methods have been investigated for reentry problems but they could only include a limited amount of uncertain parameters due to the computational cost of classical uncertainty quantification methods in high dimension. In this work we propose a method that mitigates the curse of dimensionality and allows incorporating more uncertainties to the analysis. It exploits the fact that the solver making the predictions is a system of solvers. A set of interdependent solvers, where the output of an upstream solver is directly the input of a downstream solver), each of them solving a specific aspect of the physical problem. We first build a set of approximating functions of each solver based on global criteria and then they are assembled together in order to propagate the uncertainties through the system in an efficient way. Our mathematical framework allows the identification of specific solver, that affect the accuracy of the whole system. This feature allows to build adaptively an approximation of the global system and significantly reduce the computational cost. This method is then applied to the reentry problem under study.
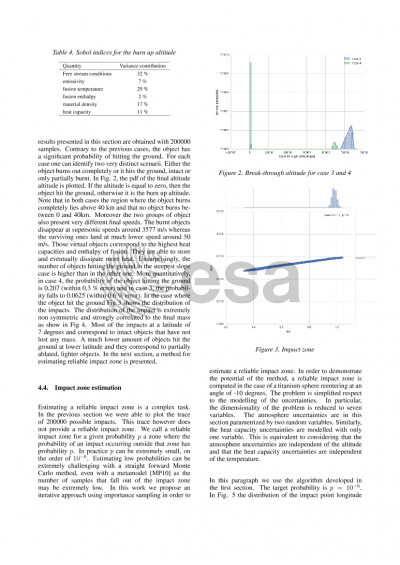
Preview