Document details

Abstract
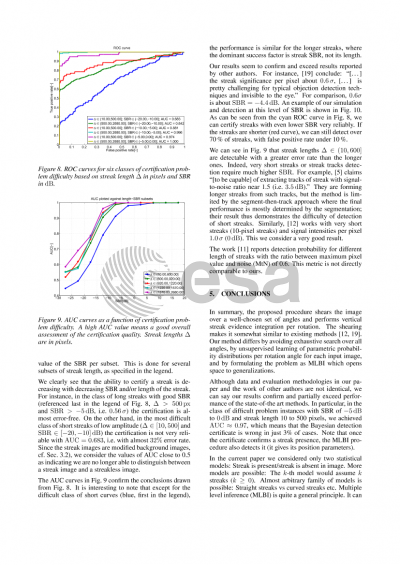
It is known that detecting straight streaks from fast moving celestial objects in optical images is an easy problem as long as the streaks are sufficiently long and/or their signal-to-background (SBR) is sufficiently high, eg. [Yanagisawa, Nakajima 2005, Zimmer et al 2013, Tagawa et al 2016].
At low signal-to-background ratio (SBR) it becomes difficult to decide on a streak presence in the image for two principal reasons: (1) as the SBR limits to zero the statistical characteristics of a streak become indistinguishable from those of the background, partly due to the finite resolution of the sensor (its limiting magnitude), (2) as the streak gets shorter then it is progressively more difficult to distinguish it from a random configuration of image background that falsely resembles a streak. A good detection procedure thus has to provide a "detection certificate" which is a yes/no answer to the question "does the image contain a streak?" The difficulty of this task stems partly from the fact that any kind of a "decision threshold" depends on image content, SBR, and sensor characteristics, so it cannot be chosen apriori. A certificate for a short streak requires a more conservative threshold but we do not know the streak length prior to detecting it, so this poses a chicken and egg dilemma. Such problems must be solved jointly, not in successive steps.
A procedure that works step-wise would first detect a candidate streak and then use a statistical test on the rest of the image to see how likely it is that a similar configuration does not appear by chance. Instead, the problem can be formulated as Two-Level Bayesian Inference [MacKay 2004]: The joint decision on identifying object parameters (streak position, length and orientation) and the statistical model that explains input data. In this work we consider only two models: streak is present/streak is absent in image. But more models are possible: the k-th model would assume k streaks (k>=0). Almost arbitrary family of models is possible: Straight streaks vs curved streaks etc. Two-level Bayesian Inference (TLBI) is quite a general principle. It can be thought of as an optimal procedure from information-theoretic point of view, a procedure that decides on the presence/detectability of an object in data. TLBI is known not to overfit [MacKay 2004].
In this paper we pose detection with certificate as a two-level Bayesian inference problem, describe the algorithm and show an experimental proof of good behavior on synthetic data and results on challenging real data.
In essence, the proposed procedure rotates the image over all angles and performs vertical streak detection per rotation. This makes it somewhat similar to existing methods [Tagawa et al 2016, Zimmer et al 2013]. Our method differs by avoiding exhaustive search over all angles, by unsupervised learning of parametric probability distributions per rotation angle for each input image, and by formulating the problem as TLBI which replaces statistical testing and opens space to generalizations.
The main steps of the detection procedure include
1. Standard image preprocessing (flat-fielding, etc).
2. Local image description by a bank of steerable filters. The filter projects image neighborhood content on a model of a short oriented streak. The filter response can be steered (rotated) to any desired orientation angle *after* computing it, so it is not necessary to repeat many image convolutions with a filter bank when searching for streak orientation.
3. Fitting a parametric statistical distribution for filter response values over the image background for every given shearing angle.
4. Composing the background distribution and a parametric streak amplitude distribution into a single streak filter response statistical distribution that does not explicitly model streak amplitude (the amplitude is marginalized out). This provides a better setup for statistical testing than assuming the streak is an outlier to the background model used in a statistical test since we can incorporate prior knowledge on the amplitude.
5. Shearing the steerable filter bank response over a set of angles (shearing is faster to compute than rotation [Tagawa et al 2016])
6. A fast dynamic programming procedure for vertical streak detection and for computing probability ratio for the two models (a streak present/no streak present).
7. A fast and efficient quasi-branch-and-bound optimization procedure over shear angles that does not need an exhaustive search over the angles but still guaranteed that global optimum is found at very accurate angular resolution.
TLBI can be applied to streak detection problems in other modalities like radio-frequency spectrograms in which a flying object leaves a trace in frequency-time space due to the Doppler shift.
Preview