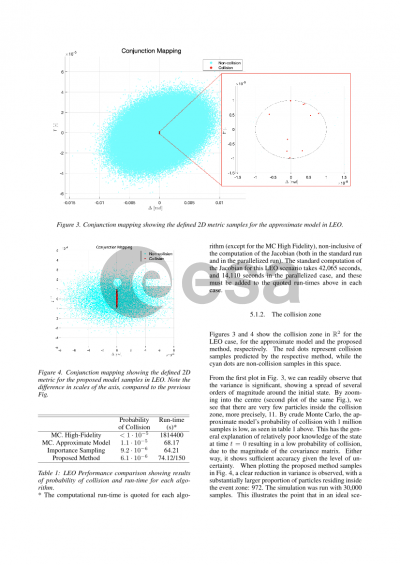
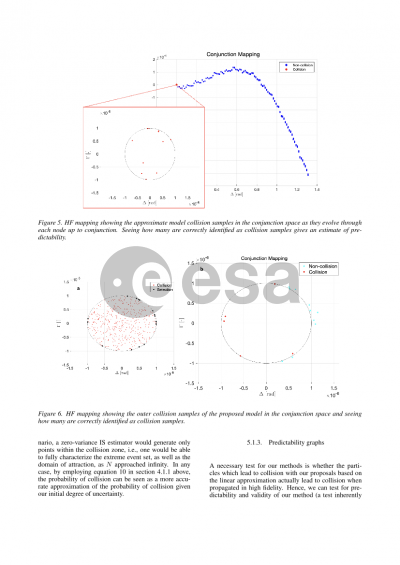
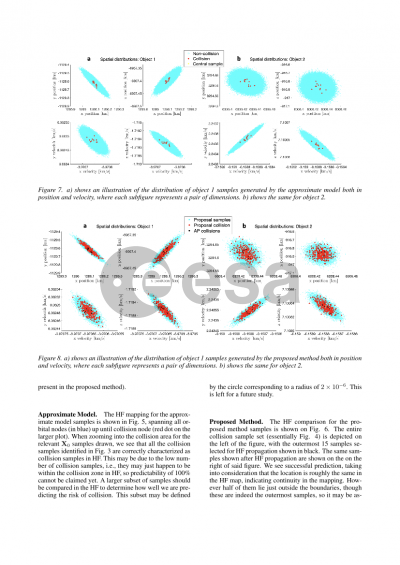
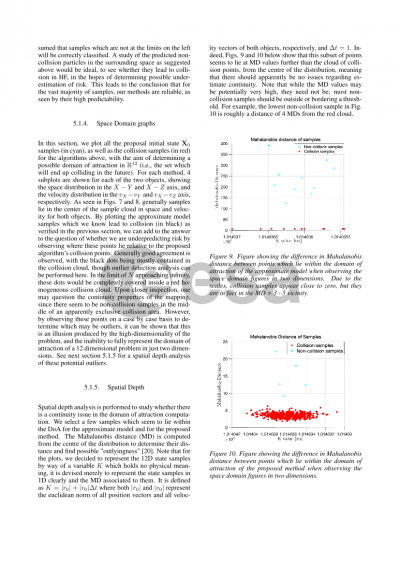
Document details

Abstract
The following abstract is relevant in the domain of Applications for Space Traffic Management.
Conjunction analysis between space objects is at the core of Space Surveillance and Tracking services provided by agencies and companies. Current methodologies have been shown to match current needs, but the number of resident space objects in highly demanded orbital regimes is expected to reach unprecedented levels. Furthermore, these methods are based on certain assumptions that must hold for computations regarding conjunction analysis to be accurate enough. The associated requirements to preserve safety and achieve automation of procedures in the rapidly changing near-Earth environment require a search for alternative approaches to improve the current state-of-the-art, and to find a suitable balance between accuracy and computational cost.
In-orbit collisions can be considered rare events, as they are seldom observed. The accurate computation of rare event probabilities has been a matter of extensive research in statistics and application fields as varied as climatology and road-traffic management and radio communications, as rare events are often those which result in the direst consequences.
In this communication, we propose a novel method for the computation of in-orbit collision probabilities. Our approach is based on the combination of rare event sampling methods with an approximate dynamical model which exploits the ease of computation of Keplerian orbital dynamics. First, a convenient two-dimensional metric is obtained by applying a transformation to the joint initial state vector of two orbiting objects, reflecting the nodal intersection of their orbital planes. By identifying, using a high-fidelity dynamical model, the node at which the objects reach the minimum separation, a linear relationship is built by applying a first-order correction to a Keplerian conjunction metric estimation, thus enabling the realisation of light-weight approximate simulations.
The probability of collision (PoC) can then be computed performing a Monte Carlo-style simulation leveraging the afore-mentioned efficiency of the approximate method.
In addition, we apply rare event sampling techniques that enable us to maximise the accuracy of the resulting estimator of the PoC for a given computational budget. The techniques used in this context include variations of importance sampling, paving the way towards Sequential Monte Carlo methods, and multi-level importance splitting schemes, which rely on the idea of approximating a very low probability as the product of larger, easier-to-compute probabilities. We will compare the probabilities obtained through the proposed methods with a high-fidelity large-scale Monte Carlo simulation that can capture collision events with the given initial conditions.
Preview