Advanced Monte Carlo Sampling Techniques for Orbital Conjunctions Analysis and NEO Impact Probability Computation

When dealing with space debris and Near-Earth Objects, the major threat for human activities and global safety is represented by possible collisions. The risk of in-orbit collisions between operative satellites and space debris, indeed, is a crucial issue in satellite operation. When a close approach is identified, it is necessary to define an indicator that can reasonably tell how risky the predicted conjunction may be, and a common practice for space agencies and satellite operators is to consider the collision probability for this purpose, together with conjunction geometry and miss-distance. On the other hand, whenever a new asteroid is discovered, it is of crucial importance to have accurate tools for detection and prediction of possible impacts. The task introduces relevant challenges due to the imperative of early detection and propagation of its state and associated uncertainty, and the problem is made even more complicated by the fact that the dynamics describing the motion of these objects is highly nonlinear, especially during close encounters with major bodies.
Present day approaches for orbital conjunctions analysis and robust detection and prediction of planetary encounters and potential impacts by NEO include simplified models or full nonlinear approaches. Simplified models significantly reduce the required computational burden, but their range of application is very narrow. On the other side, full nonlinear models (i.e. canonical Monte Carlo simulations) represent a general and flexible way of approaching collision and impact probability estimation, but they involve unavoidable intensive computations, which may not be suitable for satellite-debris daily collision probability computation or fast NEO impact probability estimation. An elegant and effective compromise was introduced by Milani, based on the concept of the line of variations.
In recent times, new advanced Monte Carlo techniques, such as the Importance Sampling (IS), Subset Simulation (SS) and Line Sampling (LS) methods were developed, aiming at reducing the computational burden by either restricting the sampling phase space or identifying optimal sampling paths within it. In parallel, an intense study on alternative uncertainty propagation methods was carried out, and innovative approaches based on the use of differential algebra (DA) were proposed.
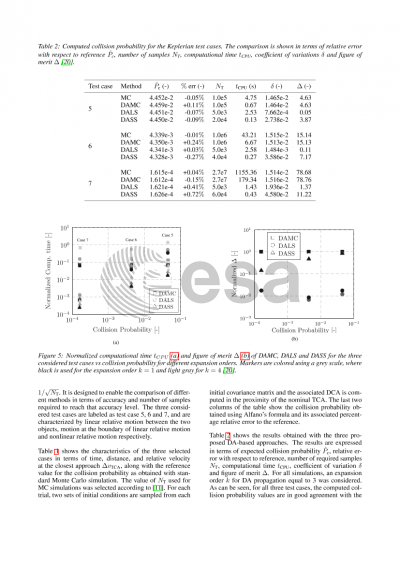
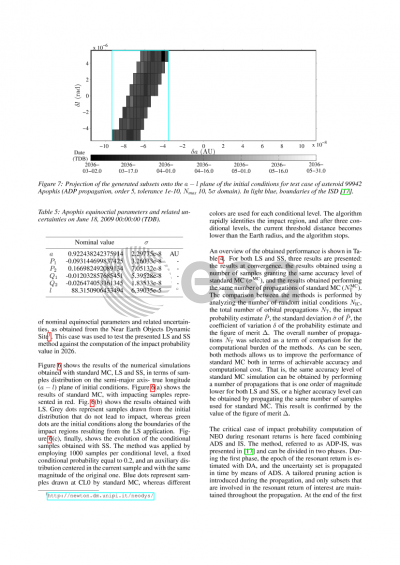
This paper presents a series of combinations and applications of the mentioned techniques to orbital conjunctions analysis and NEO impact probability computation. The problem of orbital conjunctions is faced combining the mentioned SS and LS techniques with DA, obtaining a high-order, efficient tool that can be applied to any set of initial states and using any arbitrary reference frame. The challenging task of NEO impact probability computation is faced either directly applying the SS and LS techniques or combing the IS method with a DA-based automatic domain splitting algorithm. The presented approaches offer competitive results in both fields, providing a significant improvement with respect to standard MC performance while maintaining a sufficiently high level of accuracy. For all presented approaches, test cases are presented, and a detailed analysis of the performance of the proposed methods is offered.