Document details

Abstract
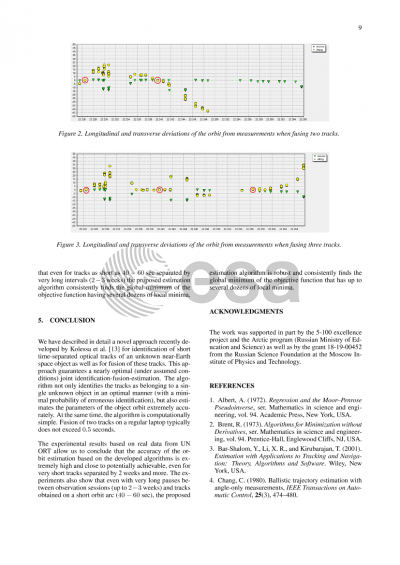
Detection and tracking of near-Earth space objects with telescopes involve sparse data, i.e., the observations related to a specific object of interest are collected only for a small fraction of the object’s orbit revolution, which is referred to as a short arc. The time-separation between successive observations of the same object can be very large (a day or more). The challenge is to estimate orbit parameters for a single track and then to improve this estimate based on a few data sets, say, fusing two tracks. Our talk addresses the problem of identification and fusion of two short optical tracks of near-Earth space objects, as well as the problem of estimation of parameters of the corresponding orbit directly from these tracks in the absence of a priori information on the object’s orbit. The popular approach to solving these problems is based on admissible regions of orbital parameters, which is typically computationally demanding. A new, purely statistical method for solving these problems is proposed. Specifically, the contribution of the talk is three-fold. First, we develop an efficient algorithm for the initial determination of an orbit based on a single track. Second, we propose a novel algorithm of estimation of orbit parameters based on two time-separated tracks. This algorithm allows one to find the global minimum of the objective function instead of localizing local minima. Third, based on the decision-theoretic approach, we develop an optimal joint track identification-estimation-fusion rule, i.e., the decision-making rule on whether the tracks belong to the same object or not that also simultaneously estimates parameters.
The work was supported in part by the Russian Ministry of Education and Science 5-100 excellence project, the Russian Federation Ministry of Education and Science Arctic program and the grant 18-19-00452 from the Russian Science Foundation at the Moscow Institute of Physics and Technology.
Preview