On the Arnold diffusion mechanism in MEO

Space debris mitigation guidelines represent the most effective method to preserve the circumterrestrial environment. Among them, end-of-life disposal solutions play a key role, and in the recent years innovative strategies have been conceived not only based on novel technologies, but also following an advanced theoretical understanding. In this context, natural perturbations are analyzed to lead the satellites towards an atmospheric reentry, reducing the disposal cost, also if departing from high-altitude regions. In the case of the Medium Earth Orbit region, home of the Global Navigation Satellite Systems, the main driver is the third-body gravitational perturbation, that can increase the eccentricity in the long term. In this way, the pericenter altitude can get into the atmospheric drag domain and the satellite can eventually reenter.
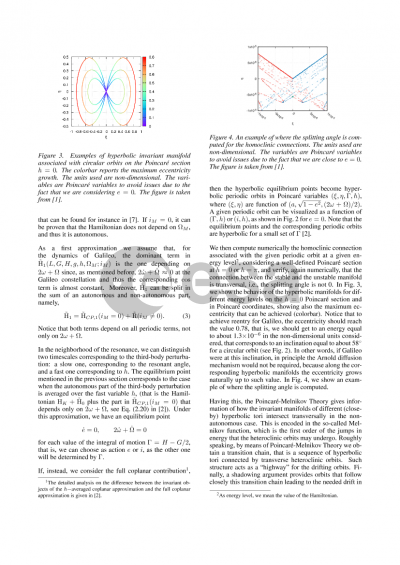
Several works have shown numerically this phenomenon, trying to link it with a chaotic behavior due to overlapping orbital resonances or to hyperbolic invariant manifolds associated with a single one. In this work, we aim at providing a robust theoretical framework that can be applied to explain the numerical outcomes.
In detail, we will show how to build an Arnold diffusion mechanism, that can trigger the eccentricity growth. Focusing on the case of Galileo, we consider a hierarchy of Hamiltonian models, assuming that the main perturbations on the motion of the spacecraft are the oblateness of the Earth and the gravitational attraction of the Moon. First, the Moon is assumed to lay on the ecliptic plane and periodic orbits and associated stable and unstable invariant manifolds are computed for various energy levels, in the neighborhood of a given resonance. Along each invariant manifold, the eccentricity increases naturally, achieving its maximum at the first intersection between them. This growth is, however, not sufficient to achieve reentry. By moving to a more realistic model, where the inclination of the Moon is taken into account, the problem becomes non-autonomous and the satellite is able to move along different energy levels. Under the ansatz of transversality of the stable and unstable manifolds in the autonomous case, checked numerically, Poincaré-Melnikov techniques are applied to show how the Arnold diffusion can be attained, by constructing a sequence of homoclinic orbits that connect invariant tori at different energy levels on the normally hyperbolic invariant manifold.