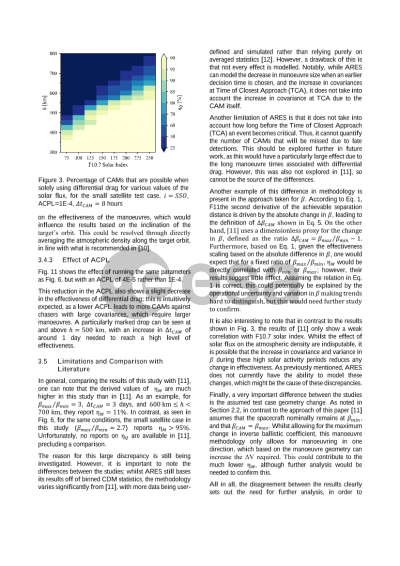
Document details

Abstract
With the increase in the number of objects in low Earth orbit (LEO), effective implementation of collision avoidance manoeuvres (CAMs) is becoming more and more critical. However, manoeuvres of this kind traditionally require a propulsion system, which can have a significant system cost for small satellites.
An alternative to standard propulsive manoeuvring is differential drag. This is the modification of trajectory through changes in the effective drag cross-sectional area, modifying the effect of the drag force on a spacecraft. This can be for instance achieved through a change in spacecraft attitude, which can in principle be accomplished without a propulsion system. However, being based on the drag force, the magnitude of the force is very small, and scales with the atmospheric density. This leads to very long manoeuvre times being needed, subject to very large variations with the altitude and solar activity.
There have been many studies on how differential drag can be used for manoeuvres during commissioning, and this has been used in practice on several occasions. However, it has remained uncertain under what conditions it is possible for differential drag to provide a sufficient trajectory change within the strict timeframe of at most a few days needed for a CAM. There have been a handful of attempts to assess its effectiveness using demonstrations in orbit, and only one case of operational usage in a fleet.
Recently, simplified analytical equations were created in order to assess the possible change in trajectory and therefore viability of a differential drag CAM. However, these have focussed on operational use, built to process single CDMs. However, these equations are being implemented in ARES (Assessment of Risk Event Statistics), as part of the development of ESA’s Debris Risk Assessment and Mitigation Analysis (DRAMA) software. This provides the unique opportunity for ARES’ statistical handling of conjunction risk analysis to be applied to the study of differential drag.
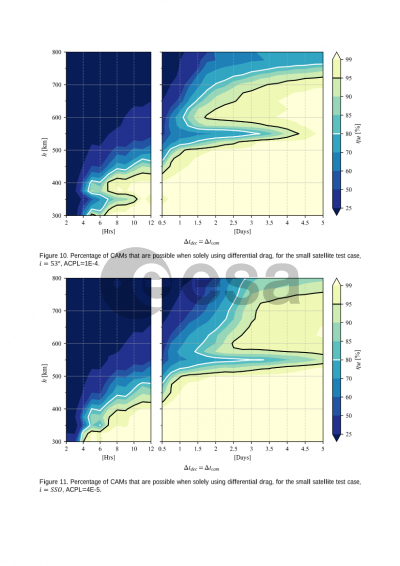
Within this work, the ARES implementation was expanded to directly compute the statistical annual number of manoeuvres and collision risk reduction possible for a spacecraft solely using differential drag to perform CAMs. An interpretable measure of effectiveness was built through the comparison to the nominal case of the same satellite with impulsive propulsion capabilities. Additionally, the exponential atmospheric model within ARES was expanded through the creation of a surrogate atmosphere model based on NRLMSIS2.0, allowing for the effects of solar activity to be considered.
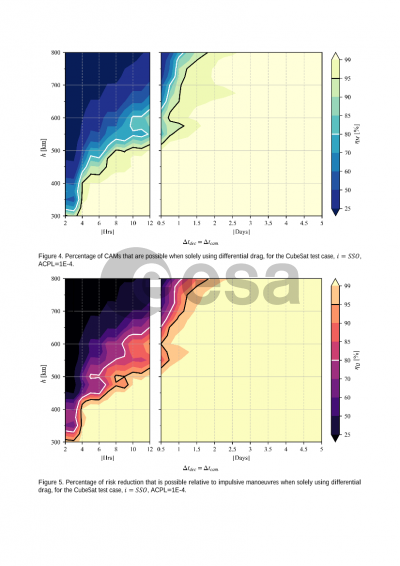
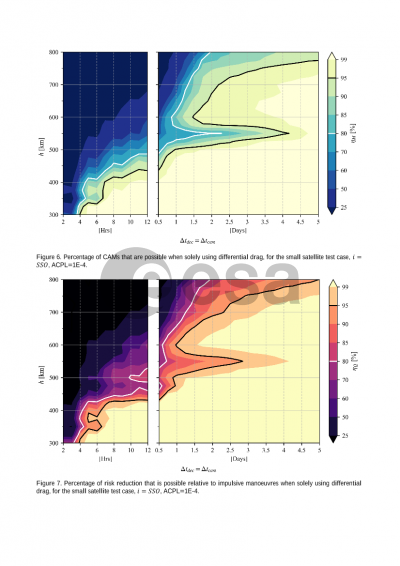
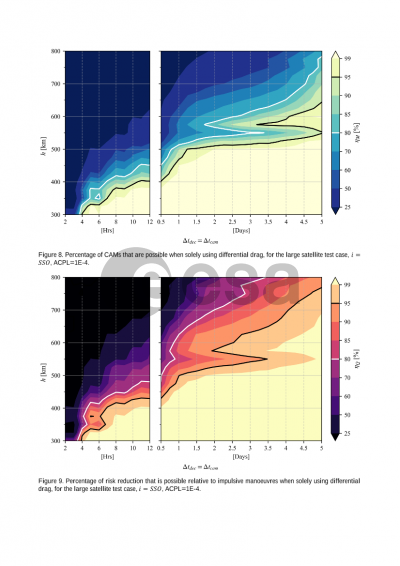
Results are then obtained through a series of parametric simulations over a series of orbital elements, environmental conditions and operational protocols, using several representative test satellites. The combination of the statistical approach and parametric sweep allows for a first “map” to be drawn across LEO of the effectiveness of differential drag. There results provide insights to mission designers and regulators, providing quantitative answers to the questions of how much notice would be needed and the proportion of high-risk alerts that could not be actioned.
Finally, limitations of the current approach are presented, outlining gaps that future developments can seek to address.
Part of this work was completed during a secondment of the first author to the UK Space Agency, within the Office of the Chief Engineer (OCE), whilst he was employed by the European Space Agency.
Preview