Document details

Abstract
With the increasing of human space exploration activities, the number of resident space objects, especially near-Earth objects, has increased dramatically. As of February 2020, there are approximately 34000 space objects in near-Earth orbit with a diameter greater than 10cm and 900000 space objects with a diameter of 1-10cm; the number of space targets with a diameter of less than 1cm exceeds 100 million. Crowded space targets will collide and explode to generate a large amount of space debris, which affects the normal activities of humans, so we need to monitor and track the space targets.
For space targets, the main observation method is to use optical sensor, such as Charged Coupled Devices (CCD) and Complementary Metal-Oxide-Semiconductor (CMOS) detectors, to observe. For optical sensors, there are two observation modes: star tracking mode and target tracking mode to track target and take images for them accordingly. For the star
tracking mode, the camera’s field view is aimed at the star and the space objects is displayed as streak in the image. For the target tracking mode, the camera’s pointing always follows the space target and the target is then shown as a source point on the image. In the two target observation modes, the most important thing to track and detect the space target is to determine the center of target position.
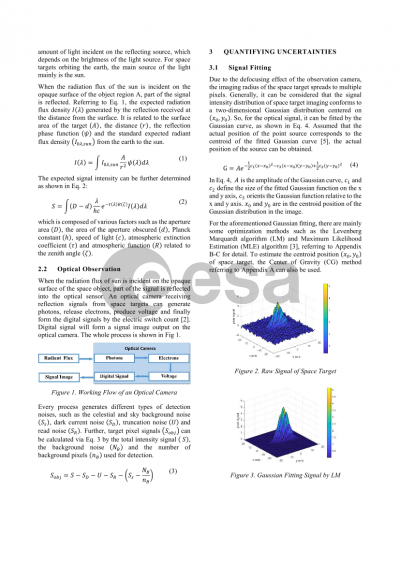
Our work mainly aims to simulate the process of camera observing the space objects for two observation mode and analyze the uncertainty of the center position of the space target. It is specifically divided into the following two parts of the content. The first, the working process of the camera is simulated, including processes of photon receiving, electron
releasing, voltage generation, modulus conversion counting and so on. The real-world noise sources are added into these processes, hence to generate realistic intensity of the optical signal. The second, Assuming the aforementioned optical signal is contaminated by pure Gaussian noise, we then carry out Gaussian fitting for the camera optical signal. As a result, the center point position of the space target in the pixel space is calculated, and its associated uncertainty is estimated accordingly via an analytic formulation derived by the inverse of the Fisher information matrix. There are a variety of methods of the center point position
uncertainty estimation, such as Iterative Weighted Center of Gravity, Least Squares 2D optimization, Maximum Likelihood Estimation and Gaussian Grid Algorithm so on. But each of them has some limitations. The limitations of the Iterative Weighted Center of Gravity and Least Squares 2D optimization are both the large amount of calculation and the dependence on the choice of the initial centroid. In addition, the Iterative Weighted Center of Gravity also depends on whether the Probability Distribution Function is well formed. For Maximum Likelihood Estimation, because the noise itself is difficult to be completely modeled, there is
a certain error in the centroid estimation. Gaussian Grid Algorithm is more suitable for the case of fewer pixels, there may be a certain deviation in the calculation of more pixels. Afterwords, pixel uncertainty of the center position is transformed to the angular measurement space (e.g., right ascension and declination) in the topocentric coordinate
system.
Our innovation lies in the uncertainty quantification method of the camera signal center point. We propose a new hybrid algorithm by combining the Maximum Likelihood Estimation and the Least Squares 2D optimization. The specific performance is that the former mainly
provides an initial centroid estimation parameter, and the latter performs further optimization, which enables more accurate uncertainty quantification of the signal centroid, especially when the signal-to-noise ratio is relatively high.
Preview