Automatic Domain Pruning Filter for Optical Observations on Short Arcs

The total number of active satellites, rocket bodies, and debris larger than 10 cm is currently about 20,000. Considering all resident space objects larger than 1 cm, this rises to an estimated minimum of 500,000 objects. Latest generation sensor networks will be able to detect small-size objects, producing millions of observations per day. Due to observability constraints, it is likely that long gaps between observations will occur for small objects. Even when observations are acquired on a single arc, it is fundamental to determine the space object orbit and accurately describe the associated uncertainty. Then, this is used to re-observe the object and update the orbit knowledge when new observations are acquired.
Filters that implement the latter task are widely used. The classical estimator used in orbit determination is the extended Kalman filter (EKF). It assumes Gaussian distribution. In contrast, the particle filter (PF) is a completely nonlinear Bayesian estimator that can approximate any probability density function by using samples. The PF proves to outperform the EKF in terms of reliability when the system is highly nonlinear. The price of its reliability is a considerable computational effort. In fact, particle filters suffer from the need to propagate a large number of samples.
The aim of this work is to implement a maximum likelihood Bayesian estimator that can cope with highly nonlinear systems (e.g. an orbiting body) and process sequential measurements yielding subsequent estimates of the state vector. For this purpose, the algorithm takes advantage of high-order Taylor expansions enabled by differential algebra (DA).
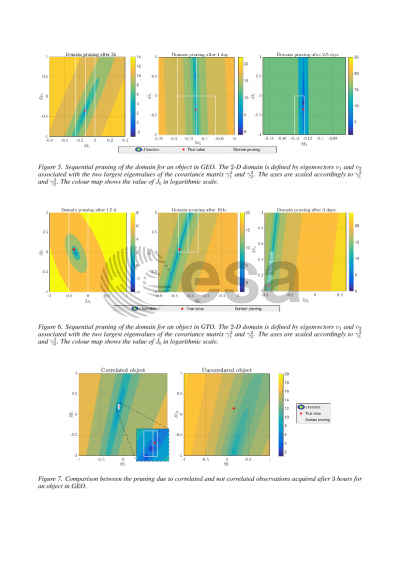
The estimator is initialized by applying least squares (LS) technique to a batch of initial observations. LS provides a solution and more importantly a confidence region, which is crucial for the initialization of the estimator and thus its effectiveness. The high order polynomial expansion of the residuals with respect to the state, computed by DA, is used to properly describe the confidence region, going beyond classical Gaussian distributions. However, the confidence region of the LS solution for very short arcs is typically large and nonlinearities play a key role in its accurate representation. When this region is propagated forward to the next available observation, automatic domain splitting techniques are employed to keep the accuracy of the propagated set higher than a prescribed threshold. As a results, a set of boxes in the phase space are available at the time of a new measurement. The evaluation of the likelihood function on each of the propagated boxes is used to prune away those boxes in which the probability of finding the object is below a given threshold. This procedure is repeated until the uncertainty region is reduced to a dimension that allows for the use of classical filtering techniques (e.g. PF). The performances of the proposed approach are assessed using real observations for GEO objects obtained with the TFRM telescope.